A theory for unifying link prediction heuristics

Definition 1. (Enclosing subgraph)
- graph $G = (V, E)$
- $x, y \in V$
- $G^{h}_{x,y}$ = h-hop enclosing subgraph for (x, y)
Theorem 1.
- high-order heuristics를 학습하면 small h도 실현 가능
- γ-decaying heuristic가 h-hop enclosing subgraph로 아주 잘 근사할 수 있음
- 거의 모든 high-order heuristics가 γ-decaying heuristic으로 통합될 수 있음
Code
아래 깃헙 코드를 확인해보면 dgl 라이브러리를 사용하여 간단하게 dgl.node_subgraph로 subgraph를 얻는 것을 확인할 수 있다.
# https://github.com/dmlc/dgl/blob/master/examples/pytorch/seal/sampler.py
class SEALSampler(object):
...
def sample_subgraph(self, target_nodes):
"""
Args:
target_nodes(Tensor): Tensor of two target nodes
Returns:
subgraph(DGLGraph): subgraph
"""
sample_nodes = [target_nodes]
frontiers = target_nodes
for i in range(self.hop):
frontiers = self.graph.out_edges(frontiers)[1]
frontiers = torch.unique(frontiers)
sample_nodes.append(frontiers)
sample_nodes = torch.cat(sample_nodes)
sample_nodes = torch.unique(sample_nodes)
subgraph = dgl.node_subgraph(self.graph, sample_nodes)
...SEAL: An implemetation of the theory using GNN
다음 3 step으로 진행된다.
1) enclosing subgraph extraction
2) node information matrix construction
3) GNN learning
GNN은 일반적으로 (A, X)를 입력으로 받는다. A는 enclosing subgraph의 adjacency matrix(인접행렬)이고 X는 node information matrix이다. 그리고 matrix X는 3가지 components (structural node labels, node embeddings and node attributes)를 가진다.
Node labeling
- Double-Radius Node Labeling (DRNL)을 제안
- node $i$에 주는 label을 $f_l (i)$라 한다면 수식을 다음과 같이 나타낸다.
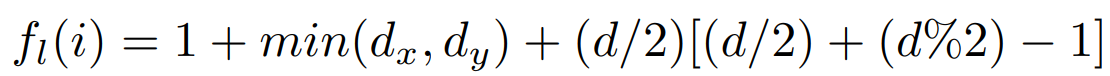
# https://github.com/dmlc/dgl/blob/master/examples/pytorch/seal/utils.py
def drnl_node_labeling(subgraph, src, dst):
"""
Double Radius Node labeling
d = r(i,u)+r(i,v)
label = 1+ min(r(i,u),r(i,v))+ (d//2)*(d//2+d%2-1)
Isolated nodes in subgraph will be set as zero.
Extreme large graph may cause memory error.
Args:
subgraph(DGLGraph): The graph
src(int): node id of one of src node in new subgraph
dst(int): node id of one of dst node in new subgraph
Returns:
z(Tensor): node labeling tensor
"""
adj = subgraph.adj_external().to_dense().numpy()
src, dst = (dst, src) if src > dst else (src, dst)
idx = list(range(src)) + list(range(src + 1, adj.shape[0]))
adj_wo_src = adj[idx, :][:, idx]
idx = list(range(dst)) + list(range(dst + 1, adj.shape[0]))
adj_wo_dst = adj[idx, :][:, idx]
dist2src = shortest_path(
adj_wo_dst, directed=False, unweighted=True, indices=src
)
dist2src = np.insert(dist2src, dst, 0, axis=0)
dist2src = torch.from_numpy(dist2src)
dist2dst = shortest_path(
adj_wo_src, directed=False, unweighted=True, indices=dst - 1
)
dist2dst = np.insert(dist2dst, src, 0, axis=0)
dist2dst = torch.from_numpy(dist2dst)
dist = dist2src + dist2dst
dist_over_2, dist_mod_2 = dist // 2, dist % 2
z = 1 + torch.min(dist2src, dist2dst)
z += dist_over_2 * (dist_over_2 + dist_mod_2 - 1)
z[src] = 1.0
z[dst] = 1.0
z[torch.isnan(z)] = 0.0
return z.to(torch.long)Incorporating latent and explicit features
sampled positive training links ($E_p \subseteq E$)와 sampled negative training links ($E_n \cap E = \varnothing$) 를 주고 학습을 시키면 link existence information를 빠르게 찾아내며 그에 맞게 최적화된다. 하지만 이런 결과는 generalization(일반화) 성능에 좋지않아 하나의 트릭을 적용했다.
negative injection
negative training link를 E에 추가하여 $G^` = (V, E \cup E_n)$에서 embedding을 만들어 성능을 향상시켰다.
* dgl.dataloading.negative_sampler를 사용하여 적용할 수 있다.
리뷰를 마치며...
link prediction task에 관심을 가지고 리뷰를 하게된 이유는 어떤 도형, 선(line)으로 이루어진 2D shape이 있다면 close 상태인지 open 상태인지를 구별할 수 있지 않을까 라는 생각을 시작으로 알아보게 되었다. 예를 들어서 사각형이 4개의 선(line)으로 이루어져있고 실제로 눈으로 ㅁ과 같이 사각형으로 보이긴 하지만 실제로는 각 선(line)의 끝점이 아주 미세하게 일치하지 않을 수가 있다. 즉, open되어 있는 상태이기때문에 link prediction을 통해 끝점(node)들을 연결할 수 있지 않을까 생각된다.
[reference]
https://github.com/dmlc/dgl/blob/master/examples/pytorch/seal/sampler.py
https://towardsdatascience.com/seal-link-prediction-explained-6237919fe575