RNN 기반 seq2seq 모델의 문제
- 하나의 고정된 크기의 벡터에 모든 정보를 압축하려고 하니까 정보 손실이 발생
- 기울기 소실(vanishig gradient) 문제가 존재
Attention Idea
- 디코더에서 출력 단어를 예측하는 매 time step마다 인코더에서의 전체 입력 문장을 다시 한 번 참고
- 전체 입력 문장을 전부 참고하는 것이 아닌해당 시점에서 예측해야할 단어와 연관이 있는 입력 단어 부분을 좀 더 attention
Attention function
Q = Query : 모든 시점의 디코더 셀에서의 은닉 상태
K = Keys : 모든 시점의 인코더 셀의 은닉 상태들
V = Values : 모든 시점의 인코더 셀의 은닉 상태들

1. 쿼리(Query)에 대해서 모든 키(Key)와의 유사도를 각각 구함
2. 구한 유사도를 키와 매핑되어있는 값(Value)에 반영
3. 유사도가 반영된 값(Value)을 모두 합하여 리턴 = Attention Value
Dot-Product Attention

1. Attention Score

인코더에서 각각의 time step의 hidden state들을 h1,h2,...,hn 이라고하고 디코더의 현재 time step의 hidden state를 st라고 하자. 또한 인코더의 hidden state와 디코더의 hidden state의 차원이 같다고 가정한다.
그리고 시점 t에서의 출력 단어를 예측하기 위해서 디코더 셀은 t-1의 hidden state와 t-1의 출력 단어를 입력값으로 받는다. 그런데 attention mechanism에서는 출력 단어 예측에 attention value라는 값도 필요로 한다.
attention value를 구하기 전에 attention score를 구해야하는데 attention score는 현재 디코더의 시점 t에서 단어를 예측하기 위해 인코더의 모든 hidden state 상태 각각이 디코더의 현 시점의 hidden state st와 얼마나 유사한지를 판단하는 score 값이다.
이 attention score를 구하기 위해 st와 인코더의 각 hidden state 간에 dot product를 수행한다. 또 다른 방법으로 concat으로 구하는 방법도 존재한다. 수식으로 정리하면 다음과 같다.

- general: t 시점의 디코더 hidden state를 transpose한 값 · 가중치 · 인코더의 각 hidden state
- concat: 선형 변환을 위한 벡터 · tanh(가중치 · concat(t 시점의 디코더 hidden state · 인코더의 각 hidden state))
concat으로 계산하는 방법에서 vTa를 곱해주는 이유는 최종값으로 스칼라 값이 나와야하기 때문이다.
2. Attention Distribution
구한 attention score는 softmax함수를 적용하여 확률 분포를 얻는다. 이것을 attention distribution이라고 한다. 그리고 각각의 값은 attention weight라고 한다.

위의 직사각형의 크기는 각 인코더의 hidden state에서의 attention weight의 크기를 나타낸다. 따라서 attention weight가 클수록 직사각형의 크기가 크다.
3. Attention Value
attention의 최종 결과값인 attention value를 얻기 위해서 각 인코더의 hidden state와 attention weight들을 곱하고 더해준다. 즉, Weighted Sum을 진행한다. 수식으로 나타내면 다음과 같다.

- at: attention value
- ati: i 시점에서의 attention weight
- hi: i 시점에서의 hidden state
attention value는 인코더의 context를 포함하고 있다고하여 context vector라고도 불린다.
4. Concat(Attention Value, Hidden State)

구해진 attention value는 st(현재 시점에서의 디코더 hidden state)와 concat이 되고 예측 연산의 입력으로 사용된다.
5. 출력층의 입력값 계산
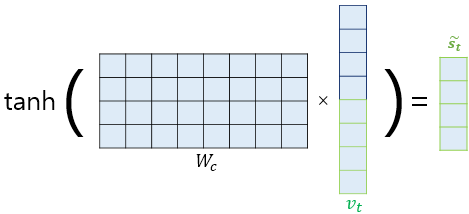
논문에서는 concatenate한 vt를 바로 출력층으로 보내기 전에 신경망 연산을 한 번 더 추가하였다고 한다. 위 그림처럼 가중치 행렬과 곱한 후에 tanh를 적용하여 새로운 벡터인 $\tilde{s}_t$ 를 구한다. 수식으로 표현하면 다음과 같다.
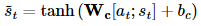
6. Prediction
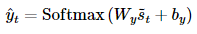
Self-Attention
앞서 설명한 seq2seq의 Attention에서 Query, Key, Value는 각각 다음과 같이 정의되었다.
Q = Querys : 모든 시점의 디코더 셀에서의 은닉 상태들
K = Keys : 모든 시점의 인코더 셀의 은닉 상태들
V = Values : 모든 시점의 인코더 셀의 은닉 상태들
그렇다면 self-attention은 무엇이고 self-attention에서의 Query, Key, Value는 무엇을 의미할까?
우선 self-attention에서의 Query(Q), Key(K), Value(V)는 모두 "입력 문장의 모든 단어 벡터"로 동일하다. 그리고 Q, K, V 간의 관계를 추출하게 된다.
좀 더 자세히 어떻게 동작하는지 알아보자.
Q, K, V는 다음과 같이 연산하여 만든다. X는 입력 단어 벡터 시퀀스를 가르키고 WQ,WK,WV는 각각 Q, K, V에 해당하는 trainable한 행렬이다.
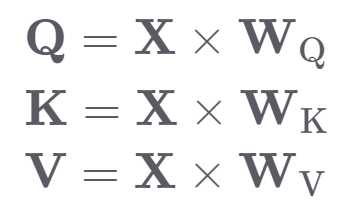
음... 예시를 하나 들어보자.
The animal didn't cross the street because it was too tired
이제 위에서 설명한 Q, K, V를 만드는 것까지 다음과 같은 순서로 진행될 것이다.
- Tokenizing
- 각 Token Embedding
- Embedding Vector Sequence의 Q, K, V를 각각 WQ,WK,WV 내적을 통해 생성
이후에 각 Q가 전체 K와의 연관성을 계산하게된다. 수식으로 나타내면 다음과 같이 될 것이다.
QKT√dk
위 예시에서 whitespace로 Tokenizing되었다고 가정하고 진행한다면 QKT는 아래처럼 각 Token의 Q마다 모든 Token의 K와 내적을 통해 score를 계산하게된다.
The · The
The · animal
The · didn't
The · cross
The · the
The · street
The · because
The · it
The · was
The · too
The · tired
animal · The
animal · animal
animal · didn't
...
"The"의 Q에 대한 각 단어의 연관성이 얼마나 되는지 score를 계산하고 "animal"도 마찬가지로 각 단어에 해당하는 score를 계산하는 식으로 진행된다.
그런데 √dk는 뭘까? dk는 key 벡터 사이즈를 의미한다. 제곱근을 왜 나누어줄까?
"Attention all you need"의 논문에 따르면 key 벡터의 차원이 늘어날수록 내적 연산시 값이 커지는 문제를 보완하기 위해서라고 한다. 또한 더 안정적인 gradient를 가지기위해서라고 한다.
그리고 각 score는 softmax 연산을 거쳐 모든 score를 양수로 만들고 그 합을 1로 만들어 준다. 여기까지를 다시 수식으로 표현하면 다음과 같다.
softmax(QKT√dk)
softmax를 거친 각 Q에 대한 모든 K의 score들은 V와 곱해진다. 즉, 다음과 같은 연산이 이루어진다.
softmax(The(Q) · The(K)) · The(V)
softmax(The(Q) · animal(K)) · animal(V)
softmax(The(Q) · didn't(K)) · didn't(V)
softmax(The(Q) · cross(K)) · cross(V)
softmax(The(Q) · the(K)) · the(V)
softmax(The(Q) · street(K)) · street(V)
softmax(The(Q) · because(K)) · because(V)
softmax(The(Q) · it(K)) · it(V)
softmax(The(Q) · was(K)) · was(V)
softmax(The(Q) · too(K)) · too(V)
softmax(The(Q) · tired(K)) · tired(V)
softmax(animal(Q) · The(K)) · The(V)
softmax(animal(Q) · animal(K)) · animal(V)
softmax(animal(Q) · didn't(K)) · didn't(V)
...
어렇게 각 score가 V와 곱해지면서 Q와 K의 연관성이 V에 반영된다. 쉽게 말하면 Q와의 연관성이 큰 K는 중요도가 클 것이고 연관성이 작은 K는 중요도가 작을 것인데 이것이 V에 반영된다는 것이다.
여기까지 다시 수식으로 정리하면 다음과 같다.
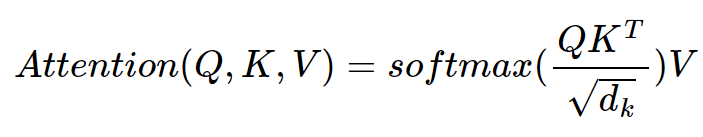
그리고 각 V는 sum이 되면 각 Token의 의미에 해당하는 값을 얻게된다. 예를 들어 "The"에 해당하는 모든 V를 더하면 전체 문장에서 "The"의 의미를 가지는 벡터를 얻게 되는 것이다.
[reference]
https://nlpinkorean.github.io/illustrated-transformer/
https://ratsgo.github.io/nlpbook/docs/language_model/tr_self_attention/