문제
문제 설명
전무로 승진한 라이언은 기분이 너무 좋아 프렌즈를 이끌고 특별 휴가를 가기로 했다.
내친김에 여행 계획까지 구상하던 라이언은 재미있는 게임을 생각해냈고 역시 전무로 승진할만한 인재라고 스스로에게 감탄했다.
라이언이 구상한(그리고 아마도 라이언만 즐거울만한) 게임은, 카카오 프렌즈를 두 팀으로 나누고, 각 팀이 같은 곳을 다른 순서로 방문하도록 해서 먼저 순회를 마친 팀이 승리하는 것이다.
그냥 지도를 주고 게임을 시작하면 재미가 덜해지므로, 라이언은 방문할 곳의 2차원 좌표 값을 구하고 각 장소를 이진트리의 노드가 되도록 구성한 후, 순회 방법을 힌트로 주어 각 팀이 스스로 경로를 찾도록 할 계획이다.
라이언은 아래와 같은 특별한 규칙으로 트리 노드들을 구성한다.
- 트리를 구성하는 모든 노드의 x, y 좌표 값은 정수이다.
- 모든 노드는 서로 다른 x값을 가진다.
- 같은 레벨(level)에 있는 노드는 같은 y 좌표를 가진다.
- 자식 노드의 y 값은 항상 부모 노드보다 작다.
- 임의의 노드 V의 왼쪽 서브 트리(left subtree)에 있는 모든 노드의 x값은 V의 x값보다 작다.
- 임의의 노드 V의 오른쪽 서브 트리(right subtree)에 있는 모든 노드의 x값은 V의 x값보다 크다.
아래 예시를 확인해보자.
라이언의 규칙에 맞게 이진트리의 노드만 좌표 평면에 그리면 다음과 같다. (이진트리의 각 노드에는 1부터 N까지 순서대로 번호가 붙어있다.)

이제, 노드를 잇는 간선(edge)을 모두 그리면 아래와 같은 모양이 된다.
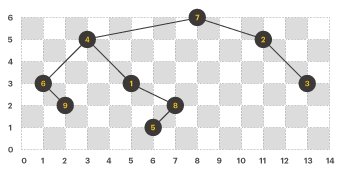
위 이진트리에서 전위 순회(preorder), 후위 순회(postorder)를 한 결과는 다음과 같고, 이것은 각 팀이 방문해야 할 순서를 의미한다.
- 전위 순회 : 7, 4, 6, 9, 1, 8, 5, 2, 3
- 후위 순회 : 9, 6, 5, 8, 1, 4, 3, 2, 7
다행히 두 팀 모두 머리를 모아 분석한 끝에 라이언의 의도를 간신히 알아차렸다.
그러나 여전히 문제는 남아있다. 노드의 수가 예시처럼 적다면 쉽게 해결할 수 있겠지만, 예상대로 라이언은 그렇게 할 생각이 전혀 없었다.
이제 당신이 나설 때가 되었다.
곤경에 빠진 카카오 프렌즈를 위해 이진트리를 구성하는 노드들의 좌표가 담긴 배열 nodeinfo가 매개변수로 주어질 때,
노드들로 구성된 이진트리를 전위 순회, 후위 순회한 결과를 2차원 배열에 순서대로 담아 return 하도록 solution 함수를 완성하자.
제한사항
nodeinfo는 이진트리를 구성하는 각 노드의 좌표가 1번 노드부터 순서대로 들어있는 2차원 배열이다.
- nodeinfo의 길이는 1 이상 10,000 이하이다.
- nodeinfo[i] 는 i + 1번 노드의 좌표이며, [x축 좌표, y축 좌표] 순으로 들어있다.
- 모든 노드의 좌표 값은 0 이상 100,000 이하인 정수이다.
- 트리의 깊이가 1,000 이하인 경우만 입력으로 주어진다.
- 모든 노드의 좌표는 문제에 주어진 규칙을 따르며, 잘못된 노드 위치가 주어지는 경우는 없다.
코드
import sys
sys.setrecursionlimit(10 ** 6) #재귀 호출 제한 설정
#Node class 정의
class Node:
def __init__(self, val, left = None, right = None):
self.val = val
self.left = left
self.right = right
preorderlist = []
postorderlist = []
#전위순회
def preorder(node):
if node is None:
return
preorderlist.append(node.val[2])
preorder(node.left)
preorder(node.right)
#후위순회
def postorder(node):
if node is None:
return
postorder(node.left)
postorder(node.right)
postorderlist.append(node.val[2])
def solution(nodeinfo):
nodes = []
x, y, n = 0, 1, 2
for idx, node in enumerate(nodeinfo):
nodes.append((node[0], node[1], idx + 1)) #x, y, n
nodes = sorted(nodes, key = lambda x : (- x[1], x[0])) #y 내림차순, x 오름차순
root = Node(nodes.pop(0)) #최상위 노드 = root
for node in nodes:
cur_node = root
while True:
#left child
if node[x] < cur_node.val[x]:
#왼쪽 자식이 있을때
if cur_node.left:
#다음 왼쪽 자식을 cur_node로 정의
cur_node = cur_node.left
continue
#왼쪽 자식이 없을때
else:
#현재 node를 왼쪽 자식으로 정의
cur_node.left = Node(node)
break
#right child
if node[x] > cur_node.val[x]:
#오른쪽 자식이 있을때
if cur_node.right:
#다음 오른쪽 자식을 cur_node로 정의
cur_node = cur_node.right
continue
#오른쪽 자식이 없을때
else:
#현재 node를 오른쪽 자식으로 정의
cur_node.right = Node(node)
break
preorder(root) #전위 순회
postorder(root) #후위 순회
return [preorderlist, postorderlist]
진행 과정
예제 #1
nodeinfo = [[5,3],[11,5],[13,3],[3,5],[6,1],[1,3],[8,6],[7,2],[2,2]]
우선 예제 #1에서 좌표 값에 따른 최상위 노드와 자식 노드를 구별해야한다.

y 좌표값이 가장 큰 요소가 최상위 노드이고 같은 y 좌표값일때 x 좌표값이 작은 쪽이 왼쪽 자식, 큰 쪽이 오른쪽 자식이 될 것이다. 따라서 코드로는 다음과 같이 정렬된다.
"nodes = sorted(nodes, key = lambda x : (- x[1], x[0]))"
이제 모든 노드들이 알맞은 위치에 정렬되었으니 최상위 노드는 첫 번째 값 [8,6]에 위치한 7이 되겠다. 그리고 7을 기준으로 트리를 구성해야한다.
트리를 구성하기에 앞서 Node에 대한 정의를 살펴봐야한다.
class Node:
def __init__(self, val, left = None, right = None):
self.val = val
self.left = left
self.right = right
val = (x, y, node 숫자) 가 되고 left는 왼쪽 자식, right는 오른쪽 자식으로 __init__이 정의된다. 간단하게 설명하자면 Node라는 type은 자기자신의 좌표, 숫자와 왼쪽 자식, 오른쪽 자식으로 구분된다라고 할 수 있다.
Node class를 정의했으니 이제 트리를 구성할 수 있다. 순서는 다음과 같다.
1) 현재 노드와 다음 노드의 x 좌표값을 비교하여 왼쪽에 위치해있는지 오른쪽에 위치해있는지에 따라서 왼쪽 자식인지 오른쪽 자식인지 판단한다.
2) 현재 노드에 자식이 없다면 다음 노드가 위치해있는 방향에 따라서 left 또는 right에 정의한다.
3) 만약 현재 노드에 이미 자식이 있다면 현재 노드의 자식을 현재 노드로 정의하고 다시 1)부터 반복한다.
트리가 완성되었으니 마지막으로 전위 순회(preorder)와 후위 순회(postorder)를 실행하면된다.
해당 코드는 매우 직관적이고 알기 쉬우므로 자세한 설명은 생략한다.
해당 문제는 트리 구조를 구현하는데 좋은 문제라고 생각한다. 다른 문제들보다 코드를 좀 길게 작성된 것은 어쩔 수 없다. 이진 탐색 트리와 트리 순회에대해 좀 더 알고 싶다면 다음 글을 확인해보길 바란다.
Python_이진 탐색 트리(BST)와 트리 순회
■ 이진 탐색 트리 (Binary Search Tree) 노드의 왼쪽 서브트리에는 그 노드의 값보다 작은 값들을 지닌 노드들로 이뤄져 있는 반면, 노드의 오른쪽 서브트리에는 그 노드의 값과 같거나 큰 값들을 지
kjy042386.tistory.com
* sys.setrecursionlimit() : 재귀 호출 깊이의 제한을 설정하는 아주 좋은 method이다
'Algorithm & Data Structure > Programmers' 카테고리의 다른 글
| [Programmers]Python_프린터 (0) | 2021.01.14 |
|---|---|
| [Programmers]Python_문자열 압축 (0) | 2021.01.13 |
| [Programmers]Python_셔틀버스 (0) | 2021.01.11 |
| [Programmers]Python_가장 긴 팰린드롬 (0) | 2021.01.10 |
| [Programmers]Python_숫자 게임 (0) | 2021.01.08 |