회귀 분석에서 손실함수로 사용되는 L2-norm(MSE)은 예측오차의 분산을 가장 최소화하는 방향으로 학습하도록 유도한다. 그리고 분류 문제에서 사용되는 교차엔트로피(cross-entropy)는 모델 예측의 불확실성을 최소화하는 방향으로 학습하도록 유도한다. 지금은 그냥 L2-norm(MSE)와 교차엔트로피를 최소화하는 방향으로 학습하도록 유도한다고 생각하자. 그렇다면 이 값들을 최소화하기위해 측정하는 방법을 알아야하는데 이 때 확률론이 필요하다.
확률론
1에서 6까지 숫자가 써있는 주사위의 각 숫자가 나올 확률이 1/6으로 똑같다고 하자. 그리고 이렇게 주사위의 각 면에 쓰인 숫자처럼 어떤 변수 X를 P(X)의 확률로 나오게 할 수 있다면, 거꾸로 말해 어떤 변수 X를 사용할 때 확률 P(X)의 값을 구할 수 있다면 이 X를 확률변수라고 말할 수 있다. 이러한 확률변수 중에는 셀 수 있을 만큼 뿔뿔이 흩어진 '이산확률변수'와 실수형태로 존재하며, 소수점 이하까지 내려가는 '연속확률변수'가 있다.
이산확률변수의 예로는 주사위의 면에 쓰인 숫자나 어떤 사건이 일어나는 시행 횟수 등이 있을 것이고 연속확률변수의 예로는 키나 몸무게, 경과 시간 등이 있다.
예를 들어 주사위를 두 번 던졌을 때 나올 숫자의 합을 확률 변수 X2라고 하고 P(X2 = 2)를 구한다고 하면 주사위가 두 번 연속으로 1이 나올 확률을 구한다는 것과 같은 말이기 때문에 1/6 * 1/6 = 1/36이 된다. 다른 값으로 X2 = 4일 때의 확률을 구한다고 하면 P(X2=4) = 3/36 = 1/12가 될 것이다. 이 과정에서 확률 변수 X2에 따라 확률이 달라지는 것을 확인했다. 이렇게 이산확률변수의 값에 따라 달라지는 확률들을 전체적으로 정리하여 나열한 것을 '이산확률분포'라고 한다.
아래 그림을 보게 되면 확률 변수 X와 Y로 나열된 확률 분포라는 것을 이해할 수 있을 것이다.

이산확률변수와 연속확률변수
이산형 확률변수는 확률변수가 가질 수 있는 경우의 수를 모두 고려한 확률을 모두 더해서 모델링한다. 수식으로는 다음과 같이 표현할 수 있다.

위와 같은 수식을 확률질량함수(Probability Mass Function, PMF)라고 한다.

이산확률분포는 위와 같은 히스토그램을 가지기 때문에 앞서 말한 확률질량함수를 사용하면 되지만 연속형 확률변수의 경우 값이 연속적이며 무한하기 때문에 연속확률분포는 아래와 같이 그려진다. 그렇기 때문에 연속형 확률변수일 경우에는 어떤 구간을 지정하여 해당 구간의 밀도를 구하여 확률을 구한다. 이때 사용하는 함수가 확률밀도함수(Probability Density Function, PDF)이다.
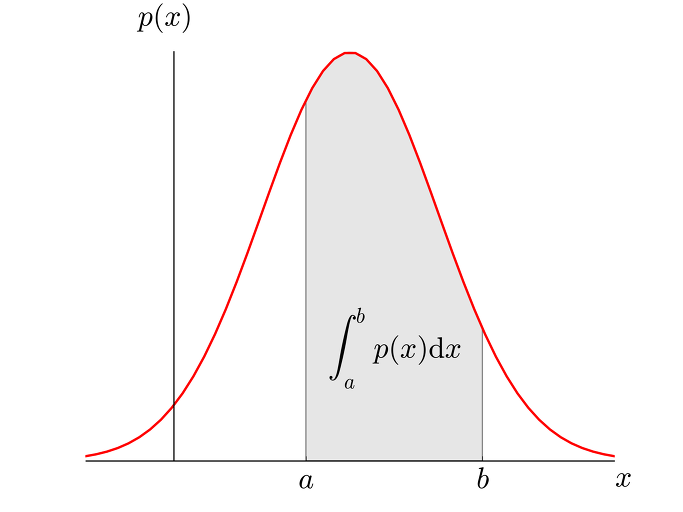
그리고 이 밀도를 구하기 위해 적분을 사용하며 수식은 위 그림의 영역 안에 작성된 것과 같다.
조건부확률
조건부확률은 사건 A가 일어난다는 것을 전제로 한 사건 B의 확률을 말하며 수식으로는 다음과 같다.

조건부확률은 소프트맥스(softmax)함수에서 각 클래스별 확률을 계산할 때 사용되고 회귀 문제의 경우 조건부기대값을 추정한다.
기대값
조건부기대값에 대해 설명하기 전 기대값이 무엇인지부터 알아보겠다. 기대값은 쉽게 말해 '나올 것이라고 예상하는 값'이다. 이산확률분포일 경우 다음과 같은 수식으로 정리할 수 있는데 여기서 f(x)가 확률 변수이고 P(x)가 확률이다. 다시 말해 f(x)가 나올 것이라고 예상하는 확률 P(x)의 기댓값이다.

연속확률분포일 경우에도 확률밀도함수와 비슷하게 적분을 사용하여 다음과 같이 계산할 수 있다.

몬테카를로(Monte Carlo) 샘플링
앞서 설명한 기대값은 확률분포를 알고 있을 때 쉽게 계산할 수 있지만 기계학습의 많은 문제들은 확률분포를 명시적으로 모를때가 대부분이다. 이럴때 데이터를 이용하여 기대값을 계산하는데 몬테카를로 샘플링 방법을 사용한다. 간단히 설명하면 반복된 무작위 추출을 이용하여 함수의 값을 확률적으로 계산하는 알고리즘이다.

특히 몬테카를로 샘플링은 이산형이든 연속형이든 상관없이 성립한다. 또한 독립적으로 샘플링을 해야하며 대수의 법칙(law of large number)에 의해 수렴성을 보장한다. 대수의 법칙이란 위 수식에서 f(x)들어가는 데이터가 커질 수록 확률이 1에 가까워진다는 정리라고 할 수 있다.
'Boostcamp AI Tech' 카테고리의 다른 글
| [Boostcamp Day-2] Python - Conditionals and Loops (0) | 2021.08.03 |
|---|---|
| [Boostcamp Day-2] Python - Function and Console IO (0) | 2021.08.03 |
| [Boostcamp Day-2] AI Math - 딥러닝 학습방법 (0) | 2021.08.03 |
| [Boostcamp Day-1] Python - variables(변수) (0) | 2021.08.02 |
| [Boostcamp Day -1] Python - 코딩 환경 (0) | 2021.08.02 |