행렬
1. 행렬이란?
행렬(matrix)은 벡터를 원소로 가지는 2차원 배열이다. 수식으로는 다음과 같이 표현할 수 있다.

python 코드로는 numpy를 사용하여 다음과 같이 구현할 수 있다.
X = np.array([[1, -1, 3], [7, 5, 0], [-2, -1, 2]])
또한 행렬은 벡터를 원소로 가지는 2차원 배열이며 행(row)과 열(column)이라는 인덱스(index)를 가진다.

벡터가 공간에서의 한 점을 의미했었는데 행렬은 여러 점들을 나타낸다.

행렬은 행렬곱을 통해 벡터를 다른 차원의 공간으로 보낼 수 있다. 간단히 말해 아래 그림과 같이 x에서 z로 보낼 수 있는 연산자(operator)라고 할 수 있다.

여기서 반대로 z에서 x로 보낼 수 있지 않을까 생각해볼 수 있다. 당연히 반대로 보낼 수 있고 이때 역행렬을 사용하면 된다.

2. 전치행렬(transpose matrix)
전치행렬은 간단히 말해서 행과 열의 인덱스가 바뀐 행렬을 말한다.

3. 행렬의 연산
행렬의 덧셈과 뺄셈, 성분곱은 벡터의 덧셈과 뺄셈, 곱셈과 똑같이 계산할 수 있다.


스칼라곱도 마찬가지로 똑같이 계산할 수 있다.

행렬 곱셈(matrix multiplication)은 i번째 행벡터와 j번쨰 열벡터 사이의 내적을 성분으로 가지는 행렬을 계산한다. 이때 아래와 같이 X의 열의 개수와 Y의 행의 개수가 같아야한다.

하지만 넘파이의 np.inner는 i번째 행벡터와 j번쨰 행벡터 사이의 내적을 성분으로 가지는 행렬을 계산한다. 즉, 수학에서 말하는 내적과는 다르므로 주의해야한다.

4. 역행렬
위에서 설명한 것 처럼 역행렬은 다른 차원으로 되돌릴 수 있는 연산자로서 사용될 수 있다. 그리고 역행렬은 행과 열 숫자가 같고 행렬식(determinant)이 0이 아닌 경우에만 계산할 수 있다. 그런데 만약 행과 열 숫자가 서로 다르다면 어떻게 해야할까? 유사역행렬(pseudo-inverse) 또는 무어-펜로즈(Moore-Penrose)역행렬을 이용한다.

또한 n이 m보다 크거나 같을때는 유사역행렬 A 와 행렬A의 곱이 단위행렬로 성립되고 반대로 n이 m보다 작거나 같을때는 행렬A의 곱이 유사역행렬 A의 곱이 단위행렬로 성립된다.
무어-펜로즈 역행렬과 같은 경우는 넘파이의 np.linalg.pnv를 이용하면 다음과 같은 연립방정식의 해를 구할 수 있다. 단, 식이 변수 개수보다 작거나 같아야한다.

그리고 다음 선형회귀식에서 y에 유사역행렬 X를 곱하여 y에 근접하는 y_hat을 찾을 수 있다.
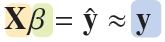
'Boostcamp AI Tech' 카테고리의 다른 글
| [Boostcamp Day-2] AI Math - 딥러닝 학습방법 (0) | 2021.08.03 |
|---|---|
| [Boostcamp Day-1] Python - variables(변수) (0) | 2021.08.02 |
| [Boostcamp Day -1] Python - 코딩 환경 (0) | 2021.08.02 |
| [Boostcamp Day-1] AI Math - 경사하강법 (0) | 2021.08.02 |
| [Boostcamp Day-1] AI Math - 벡터가 뭐에요? (0) | 2021.08.02 |