벡터
1. 벡터란?
대중적으로 벡터는 크기와 방향을 동시에 가지는 물리량이다. 수식으로는 다음과 같이 나타낼 수 있다.

또한 코드로는 다음과 같이 나타낼 수 있으며 리스트(list) 또는 배열(array)이라고 한다.
x = [1, 7, 2]
x = np.array([1, 7, 2])
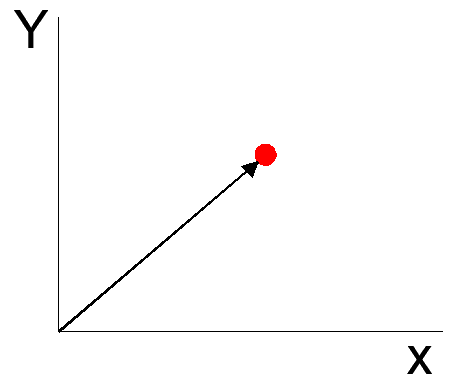
벡터는 공간 상의 한 점을 나타내며 원점으로부터 상대적인 위치를 표현한다. 아래 그림에서는 2차원 공간상의 한 점을 나타내는 것을 확인 할 수 있다.

벡터의 스칼라 곱을 해주면 벡터의 길이가 변하며 수식으로는 다음과 같이 표현할 수 있다.
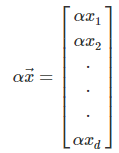
여기서 α > 1일 경우 길이가 늘어나고 α < 1일 경우 길이가 줄어든다. 만약 α < 0이라면 반대 방향이 된다.
2. 벡터의 연산
벡터의 덧셈과 뺄셈은 다음과 같이 단순히 x의 값과 y의 값을 더하거나 뺀 것과 같다.
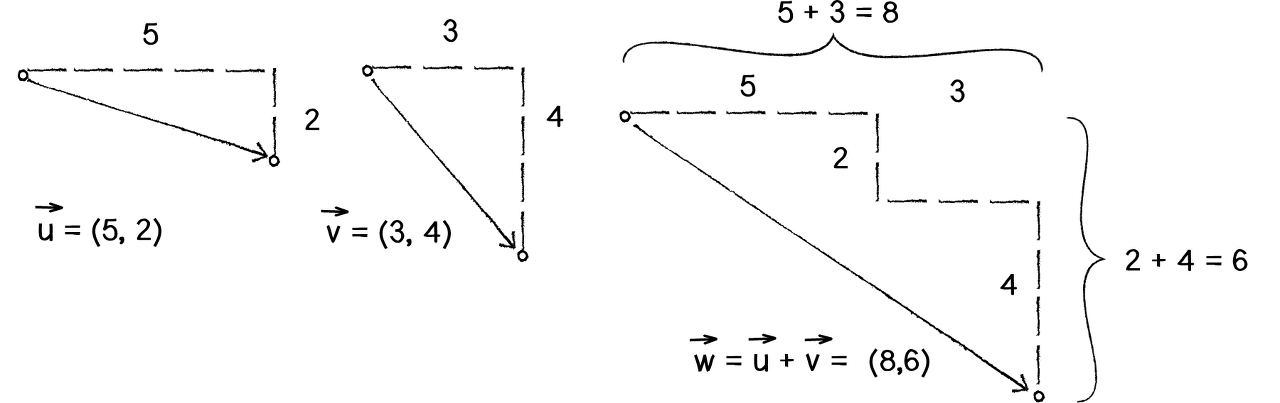
그리고 벡터의 덧셈과 뺄셈은 다음과 같이 다른 벡터로부터 상대적 위치이동을 표현한다.

벡터의 성분곱(Hadamard product)은 다음과 같이 계산할 수 있다.
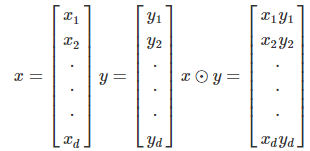
3. 벡터의 노름
벡터의 노름(norm)은 원점에서부터의 거리를 말한다.
L1-norm은 다음과 같이 절댓값을 모두 더한 것을 가르키고
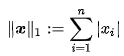
L2-norm은 다음과 같이 모든 값들을 제곱한 값을 더해서 제곱근을 씌워준 것을 말한다. 즉, 유클리드 거리를 계산하는 것과 같다.

L2-norm으로 구한 두 벡터 사이의 거리는 제2 코사인 법칙에 의해 각도를 계산하는데 이용할 수 있다.

위 제2 코사인 법칙에 의한 식의 분자는 다음과 같이 내적(inner product)으로 표현할 수 있다.

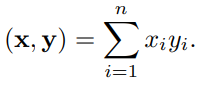
내적은 정사영(orthogonal projection)된 벡터의 길이와 관련이 있는데 우선 다음과 같이 정사영된 길이는 코사인 법칙에 의해 ||a||cosθ 가 된다.

그리고 내적은 정사영의 길이를 벡터 b의 길이 ||b||만큼 조정한 값이라고 할 수 있다. 수식으로는 다음과 같이 표현한다.

또는

마지막으로 내적은 두 벡터의 유사도(similarity)를 측정하는데 사용가능하다고 한다.
4. 노름의 기하학적 성질

위 그림과 같이 노름의 종류에 따라 기하학적 성질이 다르며 각 성질들은 필요에 따라 선택하여 사용한다.
'Boostcamp AI Tech' 카테고리의 다른 글
| [Boostcamp Day-2] AI Math - 딥러닝 학습방법 (0) | 2021.08.03 |
|---|---|
| [Boostcamp Day-1] Python - variables(변수) (0) | 2021.08.02 |
| [Boostcamp Day -1] Python - 코딩 환경 (0) | 2021.08.02 |
| [Boostcamp Day-1] AI Math - 경사하강법 (0) | 2021.08.02 |
| [Boostcamp Day-1] AI Math - 행렬이 뭐에요? (0) | 2021.08.02 |