문제
26008번: 해시 해킹
첫째 줄에 비밀번호의 길이 $N$과 문자 종류의 개수 $M$, 정수 $A$가 주어진다. ($1 \le N, M, A \le 5\,000\,000$) 둘째 줄에 재현이가 알아낸 해시값 정수 $H$가 주어진다. ($0 \le H < M$)
www.acmicpc.net
풀이
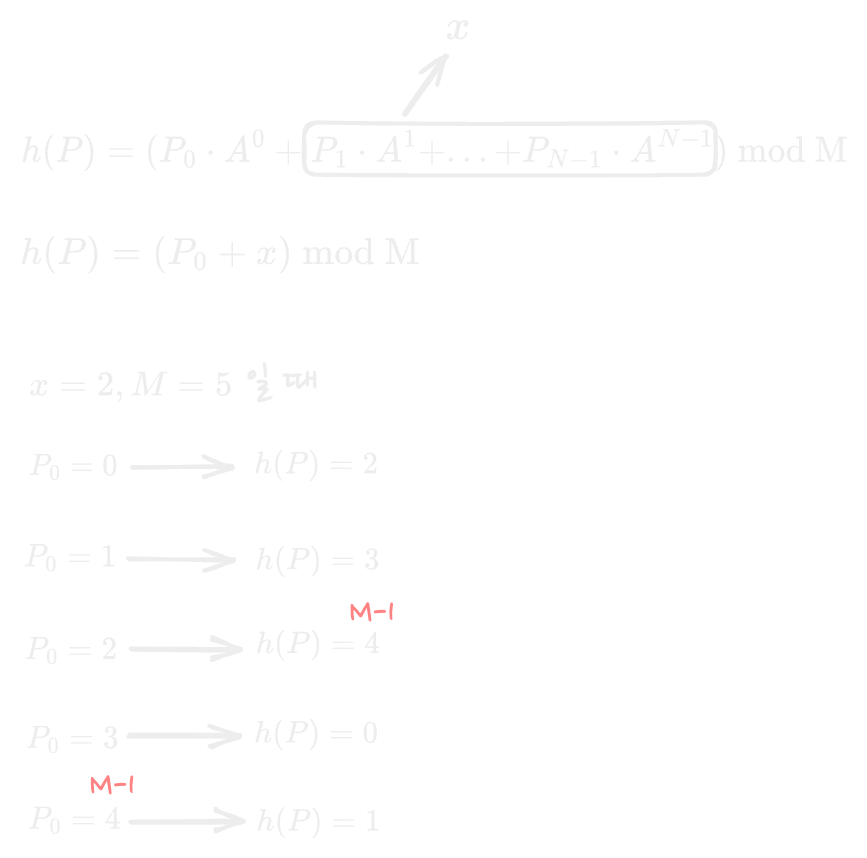
$P_1 \cdot A+...+P_{N-1}\cdot A^{N-1}$ 을 $x$라고 해보자
$x=2, M=5$일 때 $P_0$ 값을 변경함에 따라 해시 함수의 결과 값이 0 ~ M-1 으로 나오는 것을 확인할 수 있다. 즉, $P_0$ 값에 따라 $h(P)$의 결과를 원하는 값으로 만들 수 있다.
하지만 $h(P)$를 해시값 정수 H로 만들 수 있는 $P_0$는 딱 1개 밖에 없다.
대신 $P_1 \cdot A+...+P_{N-1}\cdot A^{N-1}$은 아무 값이든 가능하다. 다시 말해 $P_1, P_2, ..., P_{N - 1}$ 으로 만들 수 있는 경우의 수만큼 만들 수 있는 것이다.
결론적으로 N-1번 M개의 정수 중 하나를 고르는 경우의 수 $M^{N-1}$ 만큼 비밀번호를 만들 수 있다.
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
long answer = 1L;
int N = sc.nextInt();
int M = sc.nextInt();
int A = sc.nextInt();
int H = sc.nextInt();
for(int i = 0; i < N - 1; i ++){
answer = (answer * M) % 1000000007;
}
System.out.println(answer);
}
}Modular의 분배법칙
- (A * B) mod C = (A mod C * B mod C) mod C