로지스틱 회귀에 대해 설명하기 전 일단 시그모이드 함수에 대해서 알아보자.

시그모이드 함수는 입력값이 크면 클수록 1이라는 값으로 수렴하고, 입력값이 작을수록 0이라는 값으로 수렴하는 함수이다. 또한 0부터 1까지의 값을 가지는 특성 때문에 시그모이드의 출력값은 확률로도 사용될 수 있고, 출력값이 0.5 이상일 경우에는 참, 0.5 이하일 경우에는 거짓이라고 분류하는 분류 모델로도 사용될 수 있다.
선형 회귀의 입력값(x), 출력값 및 로지스틱 회귀의 출력값에 따른 이진 분류 결과를 표로 정리하면 다음과 같다.
[표]
| 선형 회귀 입력값(x) |
선형 회귀 출력값(wx) 로지스틱 회귀 입력값(z) |
로지스틱 회귀 출력값(y) |
이진 분류 0.5 이상: O, 0.5 이하: X |
| -2 | -2 | 0.12 | X |
| -1.5 | -1.5 | 0.18 | X |
| -1 | -1 | 0.27 | X |
| 1.25 | 1.25 | 0.78 | O |
| 1.62 | 1.62 | 0.83 | O |
| 2 | 2 | 0.88 | O |
위에 있는 표에서 볼 수 있듯이 로지스틱 회귀는 선형 회귀의 결과를 입력값으로 받아 특정 레이블로 분류하는 모델임을 알 수 있다.
로지스틱 회귀 학습
로지스틱 회귀 학습이란 현재 가지고 있는 데이터를 통해 최적의 w를 찾아내는 과정이라고 생각하면 된다. 선형 회귀에서는 랜덤한 w를 최초 부여한 후, 경사하강법으로 평균제곱오차(MSE)가 가장 작은 w를 찾아냈었다. 로지스틱 회귀 역시 경사하강법으로 최적의 w를 찾아내지만 비용함수는 크로스 엔트로피(cross entropy)를 사용한다. 그 이유는 바로 비선형성을 지니고 있는 시그모이드 함수 때문이다.
비선형
로지스틱 회귀는 선형 회귀 + 시그모이드 함수의 형태를 띠로 있으며, 시그모이드 함수의 영향으로 평균제곱오차 그래프는 아래의 그림처럼 한 개 이상의 로컬 미니멈을 가질 수 있다.

경사하강법으로 미분값이 0인 지점을 찾을 경우 운이 좋아서 글로벌 미니멈의 w를 찾을 수도 있지만 운이 나쁠 경우 로컬 미니멈의 w로 모델 학습이 마무리될 수 있다. 따라서 모델을 학습할 때 최적의 w를 항상 찾는다는 보장이 없기 때문에 평균제곱오차는 로지스틱 회귀의 적합한 비용 함수가 아니다.
크로스 엔트로피
크로스 엔트로피란 서로 다른 두 확률 분포의 차이를 의미한다. 로지스틱 회귀 관점에서는 모델의 예측값의 확률과 실제값 확률의 차이이다. 예측값과 실제값의 차이를 가장 작게 하는 w를 구함으로서 최적의 w를 구하는 방법이 바로 크로스 엔트로피이다. 공식은 다음과 같다.
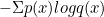
p(x)는 실제 데이터의 분포, q(x)는 모델의 예측값의 분포를 의미한다.
예를 들어 실제값과 예측값이 완전히 다른면 무한대의 값이 나올 것이고 동일하다면 0이라는 값이 나온다. 즉, 경사하강법을 사용해 크로스 엔트로피를 최저로 하는 w를 찾도록 학습하면 최적의 w를 찾게된다.
다중 분류 로지스틱 회귀
다중 분류 로지스틱 회귀는 보통 소프트맥스라고 한다. 로지스틱 회귀를 여러 개 붙여서 정규화된 출력을 함으로서 여러 개의 값을 분류할 수 있다.
'Machine Learning > Theory' 카테고리의 다른 글
| Gradient Descent(경사하강법) (0) | 2021.07.19 |
|---|---|
| 주성분 분석(Principal Component Analysis, PCA) (0) | 2021.07.13 |
| 선형회귀(Linear Regression) (0) | 2021.06.24 |
| K 평균 알고리즘(kmean++) (0) | 2021.06.22 |
| [앙상블] 배깅(bagging)과 부스팅(boosting) (0) | 2021.06.13 |