나이브 베이즈 알고리즘은 대표적인 확률 기반 머신러닝 분류 알고리즘이다. 나이브 베이즈는 데이터를 독립적인 사건으로 보고 이 사건들을 베이즈 이론에 대입시켜 가장 높은 확률의 레이블을 분류해낸다.
베이즈 이론은 다음과 같은 공식으로 표현된다.
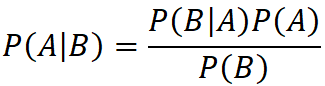
- P(A|B) : 어떤 사건 B가 일어났을 때 사건 A가 일어날 확률
- P(B|A) : 어떤 사건 A가 일어났을 때 사건 B가 일어날 확률
- P(A) : 어떤 사건 A가 일어날 확률
P(A|B)와 같이 어떤 사건 B가 일어났을 때 사건 A가 일어날 확률을 조건부 확률이라고 한다. 조건부 확률의 공식은 다음과 같다.

머신러닝에서의 나이브 베이즈 공식
P(레이블 | 데이터 특징) = P(데이터 특징 | 레이블) * P(레이블) / P(데이터 특징)어떤 데이터가 있을 때 그에 해당하는 레이블은 기존 데이터의 특징 및 레이블의 확률을 사용해 구할 수 있다.
간단한 데이터를 사용하여 위 공식을 이해 해보자.
| 시간 | 맥주 |
| 오전 | 주문 안 함 |
| 오전 | 주문 안 함 |
| 점심 | 주문함 |
| 점심 | 주문 안 함 |
| 점심 | 주문 안 함 |
| 저녁 | 주문함 |
| 저녁 | 주문함 |
| 저녁 | 주문함 |
| 저녁 | 주문 안 함 |
| 저녁 | 주문 안 함 |
저녁에 손님이 한 명 와서 주문을 할 확률은 다음과 같이 계산할 수 있다.
P(주문 | 저녁) = P(저녁 | 주문) * P(주문) / P(저녁)
= 3/4 * 4/10 / 5/10
= 0.6이제 다음과 같이 데이터의 특징을 하나 더 추가하여 두 가지 특성을 가지고 확률을 구해보겠다.
| 시간 | 성인 여부 | 맥주 |
| 오전 | 성인 | 주문 안 함 |
| 오전 | 미성년자 | 주문 안 함 |
| 점심 | 성인 | 주문함 |
| 점심 | 미성년자 | 주문 안 함 |
| 점심 | 미성년자 | 주문 안 함 |
| 저녁 | 성인 | 주문함 |
| 저녁 | 성인 | 주문함 |
| 저녁 | 성인 | 주문함 |
| 저녁 | 성인 | 주문 안 함 |
| 저녁 | 미성년자 | 주문 안 함 |
저녁에 성인손님이 와서 주문할 확률은 다음과 같이 계산하면 된다.
P(주문 | 저녁, 성인) = P(저녁, 성인 | 주문) * P(주문) / P(저녁, 성인)결합 확률
두 가지 이상의 사건이 동시에 발생하는 확률을 결합확률이라고 한다. 결합 확률의 공식은 다음과 같다.
P(A, B) = P(A|B) * P(B)하지만 나이브 베이즈 알고리즘으로 위 공식을 사용하게 되면 조건부 확률에 따른 많은 계산이 필요하게 된다. 따라서 모든 사건을 독립적인 사건으로 간주해 다음과 같은 공식으로 계산의 복잡성을 낮춘다.
P(A, B) = P(A) * P(B)모든 사건을 독립적인 사건으로 간주한다는 의미는 위 공식으로 설명하면 A가 일어날 확률과 B가 일어날 확률을 따로따로 계산하여 곱한다는 것을 말한다. 즉, A와 B가 일어날 확률이 아닌 A가 일어날 확률과 B가 일어날 확률을 독립적으로 계산하는 것을 말한다.
특징이 여러 개일 때 나이브 베이즈 공식
"(P(x1|y) * P(x2|y) * ㆍㆍㆍ * P(xn|y) * P(y)) / (P(x1) * P(x2) * ㆍㆍㆍ * P(xn))"에서 여러 확률의 곱을 나타내는 "(P(x1|y) * P(x2|y) * ㆍㆍㆍ * P(xn|y)"를 간단하게 공식화하면 다음과 같다.
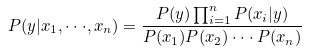
모든 레이블들은 모든 특징들의 곱이라는 공통 분모 "P(x1) * P(x2) * ㆍㆍㆍ * P(xn)"를 가지고 있다. 레이블 확률의 대소 비교만 필요한 나이브 베이즈에서는 공통 분모는 필요없기 때문에 제거하여 계산량을 줄일 수 있다.
가우시안 나이브 베이즈 분류
가우시안 나이브 베이즈 분류는 특징들의 값들이 정규 분포(가우시안 분포)돼 있다는 가정하에 조건부 확률을 계산하며, 연속적인 성질이 있는 특징이 있는 데이터를 분류하는데 적합하다. 여기서 정규 분포(가우시안 분포)는 평균값을 기준으로 좌우 완전한 대칭을 이루는 분포를 말하는 것이고 연속적인 성질이라는 말은 정수가 아닌 실수값을 가지는 데이터를 말하는 것이다.
다항 분포 나이브 베이즈(Multinomial Naive Bayes)
데이터의 특징이 출현 횟수로 표현됐을 때 사용되며 데이터의 특징이 이산적일 때 사용한다.
베르누이 나이브 베이즈 모델(Bernoulli Naive Bayes)
데이터의 특징이 0 또는 1로 표현됐을 때 사용한다. 즉, 데이터의 특징이 이산적일 때 사용한다고도 말할 수 있다.
스무딩(smoothing)
스무딩은 학습 데이터에 없던 데이터가 출현해도 빈도수에 1을 더해서 확률이 0 이 되는 현상을 방지한다.
나이브 베이즈의 장단점
- 장점
- 모든 데이터의 특징이 독립적인 사건이라는 나이브 가정에도 불구하고 실전에서 높은 정확도를 가진다. 특히 문서 분류 및 스팸 메일 분류에 강한 면모를 보인다.
- 계산 속도가 다른 모델들에 비해 상당이 빠르다.
- 단점
- 문서 분류에 적합할지는 모르나 다른 분류 모델에는 제약이 될 수 있다.
'Machine Learning > Theory' 카테고리의 다른 글
| K 평균 알고리즘(kmean++) (0) | 2021.06.22 |
|---|---|
| [앙상블] 배깅(bagging)과 부스팅(boosting) (0) | 2021.06.13 |
| 의사결정 트리(decision tree) (0) | 2021.05.30 |
| SVM(Support Vector Machine) (0) | 2021.05.25 |
| k-최근접 이웃(k-Nearest Neighbor, kNN) (0) | 2021.05.21 |